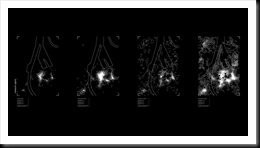
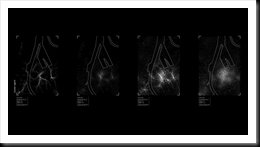
Sunday, July 5, 2009
Assignment 03A_Alice

This is my initial thought...but I am not sure if my scenairo is too complicated. Represented by simple boxes, it is imitating a situation found in a district or shopping mall.
Agent Type A represents poeple in different age groups. Therefore, in general, they are attracted/repulsed to different programmes, with different speeds.
Agent Type B (passive) represents different programmes we can found either on streets or in a shopping mall. I have just named few in the list.
Things to be defined
- Attraction Level i,e the speed and amount
- Attraction Duration i.e. how long will Agent A be attached with Agent B
- Attraction Capacity i.e. repulsion occcurs when some Agent B is over-attracted.
Differen types of Agent A should be generated randomly and being replaced along the timeline.
Wednesday, July 1, 2009
Agent-based system - applications
Here are some examples of the use and study of agent-based, self-organizing systems in architecture:
The images above are from the project Swarm Urbanism (2008) from Kokkugia, a speculative proposal which
(...) posits an urban design methodology based on the emergent capacities of Swarm Intelligence in rethinking of the current redevelopment of the Melbourne Docklands. Swarm systems involve the local interaction of autonomous agents, which give rise to emergent behavior and the self-organisation of structures. An application of swarm logic to urbanism enables a shift from notions of the master-plan to that of master-algorithm as an urban design tool. This shift changes the conception of urban design from a sequential set of decisions at reducing scales, to a simultaneous process in which a set of micro or local decisions interact generate a complex urban system. Rather than designing an urban plan that meets a set of criteria, urban imperatives are programmed into a set of agents which are able to self-organise. Consequently this conception of urbanism generates systems that are flexible to respond to the constantly changing political, economic and social pressures of urban development.
Also from Kokkugia, the above project (Emergent Fields, 2003), in which
(...) Agent-based simulation techniques are used to generate programmatic relationships and an architectonic response to this field of program. Architectural elements such as a façade, plaza, or construction grid are assigned rules or behaviours, which govern the way in which they interact with this field in the form making process. This develops an emergent relationship between program and peculiarities of architectural form, enabling the design process, and resultant architecture to exhibit particular behavioural qualities.
Also in the research developed by Space Syntax together with the Space Group at Barttlet, we can find the use of agent-based systems to explore pedestrian behaviour within the field of urbanism, flight-routes, programmatic organization, etc.
Space syntax has found that, despite many proposed higher-level cognitive models, there appears to be a fundamental process that informs human and social usage of an environment. In this paper we describe an exosomatic visual architecture, based on space syntax visibility graphs, giving many agents simultaneous access to the same pre-processed information about the configuration of a space layout. Results of experiments in a simulated retail environment show that a surprisingly simple 'random next step' based rule outperforms a more complex 'destination based' rule in reproducing observed human movement behaviour. We conclude that the effects of spatial configuration on movement patterns that space syntax studies have found are consistent with a model of individual decision behaviour based on the spatial affordances offered by the morphology of the local visual field.
Tuesday, June 23, 2009
Assignment 03A
In the first part of this assignment, you should think about the logic of a self-organizing system. You should draw diagrams and write the whole logic by which it would work. Here are some guidelines:
- Think about local intelligence and local interactions. Each agent will only "look" at its immediate surroundings and make decisions based on these "encounters". The collective intelligence comes from these local interactions (think ant colonies!)
- Define roles of your agents, or types of agents. Each agent has a set of properties and will react in a certain way when encountering certain other agents. Keep in mind the exponential complexity here: for each agent you should define the action to be taken when it encounters each of the other agents and also agents of the same type (in case there is more than one). So if you have 4 types of agents, you have to think of circa 16 types of interactions
- Think also of passive agents. Obstacles, for example, could be characterized as passive agents: they affect all other agents, but it doesn't react on any way.
- Think of forces of attraction and repulsion, and also on other more complex arrangements (in case one agent encounter a group of other agents combined, for example)
More important, use your imagination. Produce material which could explain for ANYONE about your idea, and post on the blog. Be as thorough as possible!
Please post all until Sunday, so you can have it out of the way the following week, and I can use the other week to prepare some help for you!
w07 - recap + script
Yesterday we started looking at our third and final topic: self-organizing systems and dynamics/expressions in Maya. We started some simple crowd system class, and saw some principles of dynamics in Maya (rigid bodies) and expressions (to make objects move).
Here is the script until the part we accomplish together yesterday:
In the next class we should finish it by applying fields forces (for attraction and repulsion between elements) and create the desired number of leaders and followers, connecting their dynamic forces to make them interact with each other.
Sunday, June 21, 2009
Delaunay Triangulation via Math
Here is what was supposed to be your assignment 02B, a class definition to calculate Delaunay triangulations from a set of points by means of mathematical calculations (without the help from Qhull).
There are several algorithms to approach such problem, some more efficient than others. This seems to be one of the simplest, and this class definition is based on it.
Take some time to study it and check if you understand how it is done. I'll talk about it shortly on next class.
Wednesday, June 17, 2009
w06 - recap and script
Last class we saw how to parse a Delaunay 2D text file generated by qhull and convert it to objects in Maya's stage. Here is the link from the finished script, which also contains the Delaunay3D and ConvexHull classes:
Sunday, June 14, 2009
I'm not stupid :-)


import maya.cmds as cmds
def IsBounded(item):
for x in item:
if x < 0:
return False
return True
class delauney:
def __init__(self):
self.vertices = []
self.regions = []
self.dimension = ""
self.path = "C:/MAYA/"
print "Instance of class Delauney created."
def load(self):
# Get vertices positions in the points.txt
print "Loading Qhull file..."
# Open the file and get the second line in order to get the number of vertices
f = open('C:/MAYA/points.txt', 'r')
d = f.readline()
i = f.readline()
i = int(i.strip())
# Get line by line the x, y positions (and z if it exists)
while i > 0:
l = f.readline()
t = l.split()
pt1 = float(t[0])
pt2 = float(t[1])
if len(t) > 2:
pt3 = float(t[2])
self.dimension = "3D"
self.vertices.append([pt1, pt2, pt3])
else:
pt3 = 0
self.dimension = "2D"
self.vertices.append([pt1, pt2])
i = i-1
# Feedback
print ">>> RESULTS"
print len(self.vertices), " vertices ", self.vertices
# Open the qHullResults.txt in order to get the name of the points to join.
# Get the first number, in order to get number of regions
# Daniel, I'm sorry for the hardcoding for the names of the files, and for the "region.append(int(t[2]))" if its not a 3D drawing, but i'm really tired
f = open('C:/MAYA/qHullResults.txt', 'r')
l = f.readline()
i = int(l)
# Get line by line the name of the points to join
while i > 0:
l = f.readline()
t = l.split()
region = []
j=0
while j < i:
region.append(int(t[0]))
region.append(int(t[1]))
region.append(int(t[2]))
j = j + 1
self.regions.append(region)
i = i-1
# Feedback
print len(self.regions), " regions ", self.regions
f.close()
def draw(self):
# draw a curve between the points to create the regions!
for region in filter(IsBounded, self.regions):
vs = []
neg = 0
for i in region:
if i < 0:
neg = 1
break
v = self.vertices[i]
vs.append(v)
if neg == 0:
crv = cmds.curve(ep=vs, d=1)
cmds.closeCurve(crv, rpo=1)
Saturday, June 13, 2009
this is my studio script (using classes). i wrote some more helping scripts in the beginning.
this part is running the script in way like on the video above
import maya.cmds as cmds
import maya.mel as mm
import math
import sys
from random import*
from setColor import*
sys.setrecursionlimit(8000)
############################################################################################################################
def centerOfFace(facet):
#find the vertices that define that face.
vertex = cmds.polyListComponentConversion(facet, ff=1, tv=1)
cmds.select(vertex, r=1)
vertexFlat = cmds.ls(sl=1, fl=1)
#find out how many vertices define that face
vertCount = len(vertexFlat)
#print vertexFlat
#for each vertex go through and find it's world space position.
vertPositionSumX = 0.
vertPositionSumY = 0.
vertPositionSumZ = 0.
for a in range(0, vertCount, 1):
coordinate = cmds.pointPosition(vertexFlat[a], w=1)
vertPositionSumX += coordinate[0]
vertPositionSumY += coordinate[1]
vertPositionSumZ += coordinate[2]
centroidX = vertPositionSumX/float(vertCount)
centroidY = vertPositionSumY/float(vertCount)
centroidZ = vertPositionSumZ/float(vertCount)
return [centroidX, centroidY, centroidZ]
def getDistance(start, end):
#start and end must be lists xyz
v = [start[0]-end[0], start[1]-end[1], start[2]-end[2]] #list format x,y,z
vector = "<<" + str(v[0]) + "," + str(v[1]) + "," + str(v[2]) + ">>"
mag = mm.eval("mag " + vector + ";")
return mag
def closestLocator (locator, netOfLocs):
locatorPos = cmds.pointPosition(locator)
distance = 1000000000
closLocData = []
closestLocator = ""
for i in netOfLocs:
locPos = cmds.pointPosition(i)
currDist = getDistance(locatorPos, locPos)
if currDist < distance:
distance = currDist
closLocator = i
closLocPos = locPos
closLocDist = currDist
closLocData.append (closLocator)
closLocData.append (closLocPos)
closLocData.append (closLocDist)
return closLocData
def closestLocatorToPoint (Point, netOfLocs):
locatorPos = Point
distance = 1000000000
closLocData = []
closestLocator = ""
for i in netOfLocs:
locPos = cmds.pointPosition(i)
currDist = getDistance(locatorPos, locPos)
if currDist < distance:
distance = currDist
closLocator = i
closLocPos = locPos
closLocDist = currDist
closLocData.append (closLocator)
closLocData.append (closLocPos)
closLocData.append (closLocDist)
return closLocData
def midPoint (listPt1,listPt2):
x=0
y=0
z=0
n=0
for i in listPt1:
ptPos = cmds.pointPosition(i)
x=x+ptPos[0]
y=y+ptPos[1]
z=z+ptPos[2]
n=n+1
for i in listPt2:
ptPos = cmds.pointPosition(i)
x=x+ptPos[0]
y=y+ptPos[1]
z=z+ptPos[2]
n=n+1
midX = x/n
midY = y/n
midZ = z/n
midPt=[]
midPt.append (midX)
midPt.append (midY)
midPt.append (midZ)
return midPt
def midPointInPtLocs (listLoc1,listPt2):
x=0
y=0
z=0
n=0
for i in (1,len(listLoc1)-1,1):
ptPos = cmds.pointPosition(listLoc1[i])
x=x+ptPos[0]
y=y+ptPos[1]
z=z+ptPos[2]
n=n+1
ptPos = listPt2
x=x+(ptPos[0]*len(listLoc1))
y=y+(ptPos[1]*len(listLoc1))
z=z+(ptPos[2]*len(listLoc1))
n=n+len(listLoc1)
midX = x/n
midY = y/n
midZ = z/n
midPt=[]
midPt.append (midX)
midPt.append (midY)
midPt.append (midZ)
return midPt
def direction(a,b):
"Returns the direction vector going from a to b"
# Calculate direction vector
dire = [ a[0] - b[0], a[1] - b[1], a[2] - b[2] ] # a-b
return dire
############################################################################################################################
class graves:
def __init__(self):
print "Instance of class Graves created."
def getData(self):
locs = cmds.filterExpand(sm=22)
return locs
def getRepulsiveLocs (self):
locs1 = cmds.filterExpand(sm=22)
return locs1
def getAllLocators (self, AmountOfAttractors):
repulciveLocs = cmds.filterExpand(sm=22)
locs =[]
for i in range (AmountOfAttractors):
L = repulciveLocs[0]
repulciveLocs.remove (L)
locs.append (L)
return locs, repulciveLocs
def polyCubesInLocators (self, locators, size):
cubes = []
for i in locators:
position = cmds.pointPosition(i)
cube = cmds.polyCube (w =size ,h=size ,d=size )
cmds.move (position[0], position[1], position[2], cube)
cubes.append (cube)
return cubes
def makeNet (self, locators, numRow, numCell):
allLocs = []
startLocs = []
x = randint (98,102)
x = x/100.0
for i in range (numRow):
for j in range (numCell):
newloc= cmds.spaceLocator( p=(j*10*x, i*10*x, 0) )
if i == 0:
startLocs.append (newloc)
elif i == (numRow-1):
startLocs.append (newloc)
else:
allLocs.append (newloc)
cmds.refresh()
return startLocs, allLocs
def changeNetBecauseRepulsive (self, allLocs, repulsiveLocs, repSize, pointsAmount = 4, N=0):
Empty =[]
LOCS = allLocs
for i in allLocs:
Empty.append (i)
C = pointsAmount
for k in repulsiveLocs:
for i in range (repSize):
L=(repSize/5)*(i+1)
for j in range (L):
Kpos = cmds.pointPosition(k)
closLoc = closestLocatorToPoint(Kpos, LOCS)
LOCpos = closLoc[1]
clLoc = closLoc[0]
direc = direction(LOCpos, Kpos)
newX = ((direc[0]*6)/((i+1)*(i+1)))
newY = ((direc[1]*6)/((i+1)*(i+1)))
newZ = ((direc[2]*6)/((i+1)*(i+1)))
cmds.move (newX, newY, newZ, clLoc)
LOCS.remove (clLoc)
cmds.refresh()
return Empty
def subdivStartLocs (self, startLocs, locs):
subStartLocs = []
lenLocs = len(locs)
lenStertLocs = len(startLocs)
locsPerUnit = lenStertLocs/lenLocs
for i in range (lenLocs):
groupOfLocs = []
groupOfLocs.append (locs[i])
for j in range (locsPerUnit):
numOfLoc = i*locsPerUnit+j
loccc = startLocs [numOfLoc]
loccc = loccc[0]
groupOfLocs.append (loccc)
subStartLocs.append (groupOfLocs)
return subStartLocs
def looping1 (self, subdivStartLocs, allLocs, locs, size, number, cubes):
#cmds.pause( sec=0.5 )
cmds.refresh()
size *= 1.03
color = 255/(size*10)
number = number + 1
print "number"
print number
temploryList = []
midPoints =[]
N=0
for i in subdivStartLocs:
if number == 1:
Pt1 = len(i)/2
midP = i[Pt1]
midP = cmds.pointPosition(midP)
remLocs = []
remLocs.append (i[0])
x = randint (2,len(i)+7)
else:
midP = i
remLocs = []
#remLocs.append (i)
x = randint (2,len(subdivStartLocs)+7)
n = 0
if len(allLocs)>x:
for g in range (x):
closLocData = closestLocatorToPoint (midP, allLocs)
closLocator = closLocData[0]
closLocPos = closLocData[1]
closLocDist = closLocData[2]
newSphere = cmds.polySphere (r=size, sx=4, sy=4)
cmds.move (closLocPos[0], closLocPos[1], closLocPos[2], newSphere)
remLocs.append (closLocator)
allLocs.remove (closLocator)
if len(allLocs)<2:
return "Done."
temploryList.append (remLocs)
#################################################################
if number == 1:
Pt1 = len(i)/2
midPt1 = i[Pt1]
midPt1 = cmds.pointPosition(midPt1)
ptPos = cmds.pointPosition(i[0])
midPt = midPoint (remLocs,i)
else:
ptPos = cmds.pointPosition(locs[N])
midPt = midPointInPtLocs (remLocs,i)
midX = midPt[0] - midP[0]
midY = midPt[1] - midP[1]
midX = ptPos[0] + (midX/2)
midY = ptPos[1] + (midY/2)
cmds.move (midX, midY, 0, cubes[N])
cmds.move (midX, midY, 0, locs[N])
midP = midPt
N = N+1
midPoints.append (midP)
##################################################################
subdivStartLocs = midPoints
if len(allLocs)>0:
self.looping1 (subdivStartLocs, allLocs, locs, size, number, cubes)
else:
return "Done."
g= graves()
locs, repulsiveLocs = g.getAllLocators (8)
cubes = g.polyCubesInLocators ( locs, 6)
cubes1 = g.polyCubesInLocators ( repulsiveLocs, 10)
startLocs, allLocs = g.makeNet(locs,48,48)
cubes2 = g.polyCubesInLocators ( startLocs, 1)
allLocsPPP = allLocs
ALLLOCS = g.changeNetBecauseRepulsive (allLocsPPP, repulsiveLocs, 13)
subd = g.subdivStartLocs(startLocs,locs)
g.looping1 (subd, ALLLOCS, locs, 1.2, 0, cubes)
Wednesday, June 10, 2009
Assignment 02A
- The qhull commands you need to run are already in the runQhull method of the Qhull class. You don't need to worry about them. They will return you a text file containing all the information you need to assemble your objects
- The structure of the new class should be very similar from the Voronoi class structure. You should write a load method to read the file you generated from qhull and parse it, saving vertex and region information on the regions and vertices attributes of the class.
- Then you should then concentrate on the draw function. Keep in mind some of the workarounds done in the Voronoi class, like re-ordering the vertices, are not necessary in the Delaunay or convex hull. Just read all the vertices, then draw the regions using the vertices indexes.
- You can find some help on the web. Some sites:
You should post whatever results you get on the blog by this Sunday, 14.06. You should also post any questions you might encounter.
Week 05 - script
Week 05 - recap
Monday, June 8, 2009
Week 05 - file to download
After that, we will add one more method to the class, which uses pure mathematics to perform voronoi calculations, so we can learn a bit about vector math and some other scripting techniques.
For that, you should download this script and save it in your script folder.